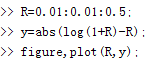最近在理财书中看到“72法则”这个概念，说的是用72除以年利率，就可以粗略得到多少年资金可以翻倍。比如一个理财年利率为4%，那么72/4=18年，18年后你的收益会翻倍。

 蜗牛做为一个工科女，很好奇如何推导的，今天有空，推导了一把数学公式，满足一下自己的好奇心。

至此，还是没有看到72的影子，上网搜了一下，原来当R很小时，log(1+R)约等于R。好吧，先来证明这个吧，数学忘得差不多了，既然不会证明，那就用曲线来证明吧。

拿出强大的MATLAB工具，写两行代码，显示一下曲线吧。

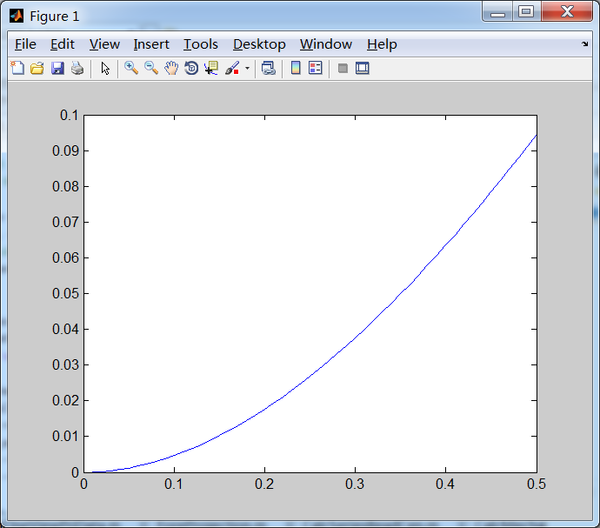
看一看MATLAB显示的结果图

x轴是年利率R从0到0.5，即0%到50%，y轴表示log(1+R)-R的绝对值，可以看出来，就算R为50%（相当高的收益率啊，）log(1+R)与R的差值也就在0.1，即10%以下，所以“log(1+R)约等于R”的结论成立。

 好吧，那这时候公式就应该写为N=0.693/R了，依然没有看到72的影子。还记得最上面说的例子吗？一个理财年利率为4%，那么72/4=18年翻倍。此处将R原有的4%变成了4，那公式就可以写成：

N=69.3/R（此处的R即仅保留%之前的数据）

69.3？好像和72还是没有关系啊？继续上网查，原来是因为72有很多公因数，比69.3方便计算，也方便记忆，所以就用72替换69.3。好吧，公式终于出来了：

N=72/R

好开心，原来“72法则”是这么来的。

总结一下吧

1. “72法则”与本金无关，只与利率有关；

2.  姐妹们可以简单的将72除以年利率，得到多少年可以资金翻倍。